みなさん、こんにちは。
最近は気温が上がり、半袖で過ごしやすい季節になってきましたね。
エルカミノではGWが明けて、久々に通常授業が始まりました。
塾生のみなさんは相変わらず、一生懸命勉強に取り組んでいました。
さて、前回のブログの問題はいかがでしたでしょうか。
本日はその解答を発表します。
それぞれ該当学年の解答は以下に記載しています。
小1~3年生向けの問題
【解答・解説】
(1)左の図のように切って並べ替えると、右の図のような、たて9㎝、横4㎝の長方形ができる。
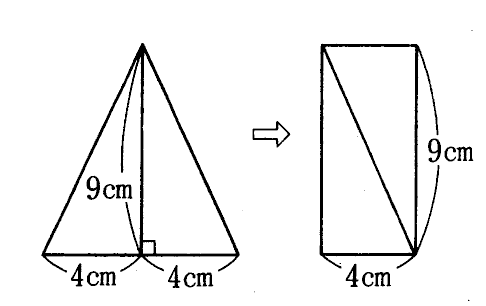
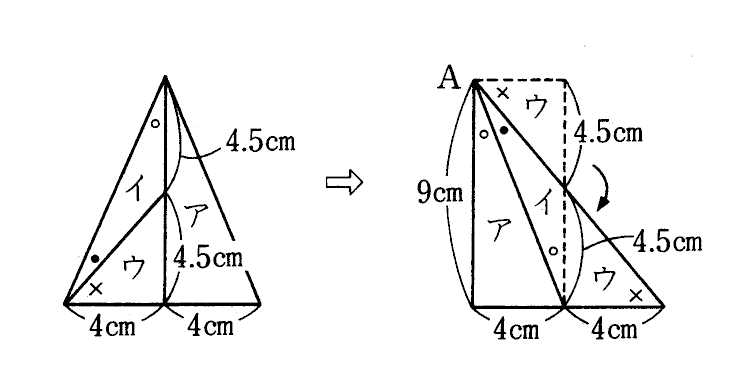
(2) (1)の長方形からたて9㎝、横8㎝の三角形を作ることを考えると右の図のように、ア、イ、ウに分割して並び替えればよい。
したがって分割の仕方は、左の図のようになる。
(3) (1)で作った長方形から1辺が6㎝の正方形を作ることを考えると、右の図のようになる。
つまりもとの三角形は、左の図のように分割すればよい。
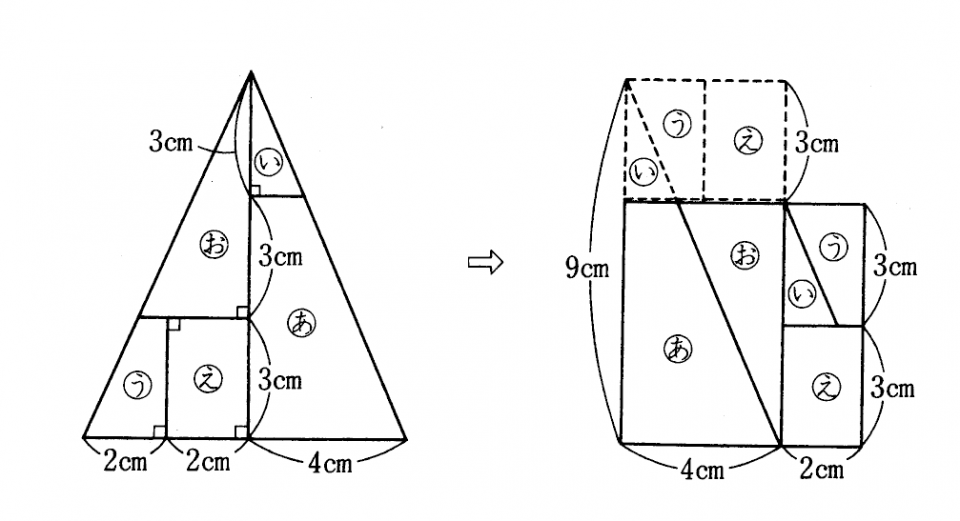
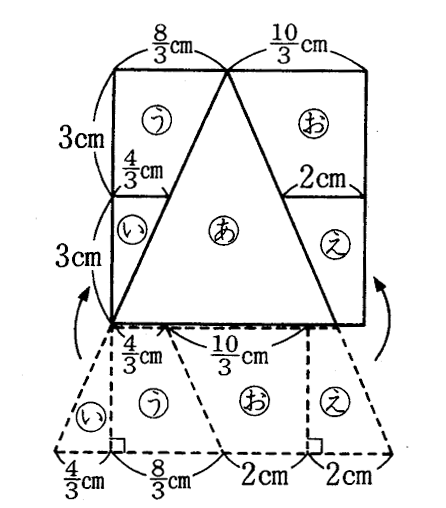
[別解]下の図のように、もとの二等辺三角形の頂点から6㎝のところで底辺に平行に切り、切り取った部分を4枚に分割し、1辺が6㎝の正方形になるように当てはめることを考える。
三角形(あ)の底辺の長さは8×6/9=16/3(㎝)だから、台形(え)の上底の長さは6-16/3=2/3(㎝)、下底は2/3+4×3/9=2(㎝)となる。同様に台形(う)の上底は4×3/9=4/3(㎝)、下底は4/3×2=8/3(㎝)となり、台形(お)の上底は6-8/3=10/3(㎝)、下底は2㎝となる。1辺が6㎝の正方形を作るにはもとの二等辺三角形の紙を(あ)~(お)のように分割して作ることもできる。
(1)左の図のように切って並べ替えると、右の図のような、たて9㎝、横4㎝の長方形ができる。

(2) (1)の長方形からたて9㎝、横8㎝の三角形を作ることを考えると右の図のように、ア、イ、ウに分割して並び替えればよい。
したがって分割の仕方は、左の図のようになる。

(3) (1)で作った長方形から1辺が6㎝の正方形を作ることを考えると、右の図のようになる。
つまりもとの三角形は、左の図のように分割すればよい。

[別解]下の図のように、もとの二等辺三角形の頂点から6㎝のところで底辺に平行に切り、切り取った部分を4枚に分割し、1辺が6㎝の正方形になるように当てはめることを考える。
三角形(あ)の底辺の長さは8×6/9=16/3(㎝)だから、台形(え)の上底の長さは6-16/3=2/3(㎝)、下底は2/3+4×3/9=2(㎝)となる。同様に台形(う)の上底は4×3/9=4/3(㎝)、下底は4/3×2=8/3(㎝)となり、台形(お)の上底は6-8/3=10/3(㎝)、下底は2㎝となる。1辺が6㎝の正方形を作るにはもとの二等辺三角形の紙を(あ)~(お)のように分割して作ることもできる。

小4~5年生向けの問題
【解答】
(1)
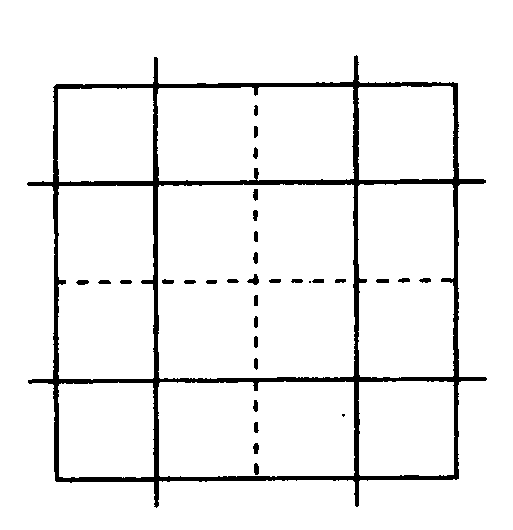
(2) 6回 (3) 508枚
【解説】
(2)操作を2回、3回行った場合は下の図のようになる。
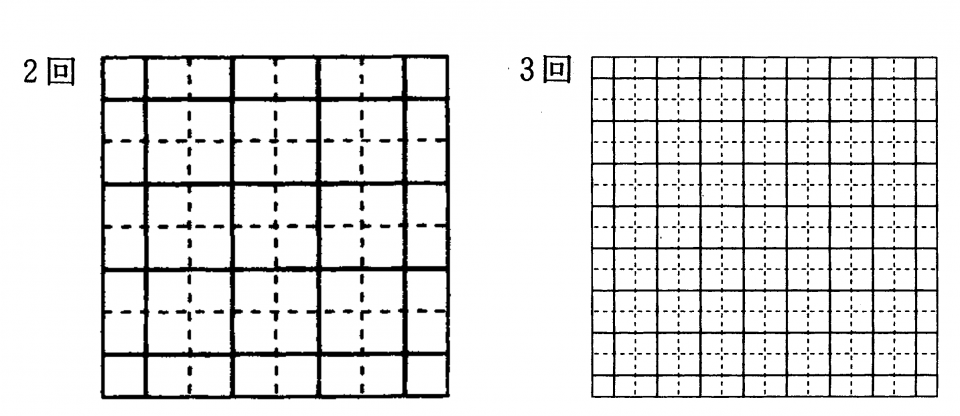
一番大きい紙の枚数は、操作を1回おこなったときは1枚、2回行ったときは3×3=9(枚)、3回行ったときは7×7=49(枚)なので、4回行うと1辺に7×2+1=15(枚)ずつ、全部で15×15=225(枚)できる。
同様に操作を5回行うと、1辺に15×2+1=31(枚)ずつできるから、全部で31×31=961(枚)と求められる。よって、一番大きい紙が1000枚以上できるのはこの操作を6回以上行った場合だから、操作を行った回数として考えられる最も小さい数は6回である。
(3)(2)と同様にして続けると、この操作を6回行ったとき一番大きい紙は(31×2+1)×(31×2+1)=3969(枚)、7回行ったときは(63×2+1)×(63×2+1)=16129(枚)できる。したがって、一番大きい紙が10000枚以上できるのはこの操作を7回以上行ったときとわかる。7回目の操作を行うと1辺に63×2+1=127(枚)並ぶので、このとき二番目に大きい紙は127×4=508(枚)できる。
(1)

(2) 6回 (3) 508枚
【解説】
(2)操作を2回、3回行った場合は下の図のようになる。

一番大きい紙の枚数は、操作を1回おこなったときは1枚、2回行ったときは3×3=9(枚)、3回行ったときは7×7=49(枚)なので、4回行うと1辺に7×2+1=15(枚)ずつ、全部で15×15=225(枚)できる。
同様に操作を5回行うと、1辺に15×2+1=31(枚)ずつできるから、全部で31×31=961(枚)と求められる。よって、一番大きい紙が1000枚以上できるのはこの操作を6回以上行った場合だから、操作を行った回数として考えられる最も小さい数は6回である。
(3)(2)と同様にして続けると、この操作を6回行ったとき一番大きい紙は(31×2+1)×(31×2+1)=3969(枚)、7回行ったときは(63×2+1)×(63×2+1)=16129(枚)できる。したがって、一番大きい紙が10000枚以上できるのはこの操作を7回以上行ったときとわかる。7回目の操作を行うと1辺に63×2+1=127(枚)並ぶので、このとき二番目に大きい紙は127×4=508(枚)できる。
小6年生向けの問題
【解答】
(1)
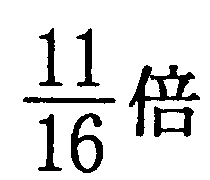
(2)
(3)
【解説】
(1) 折ってできた図形は下の図のような五角形になる。
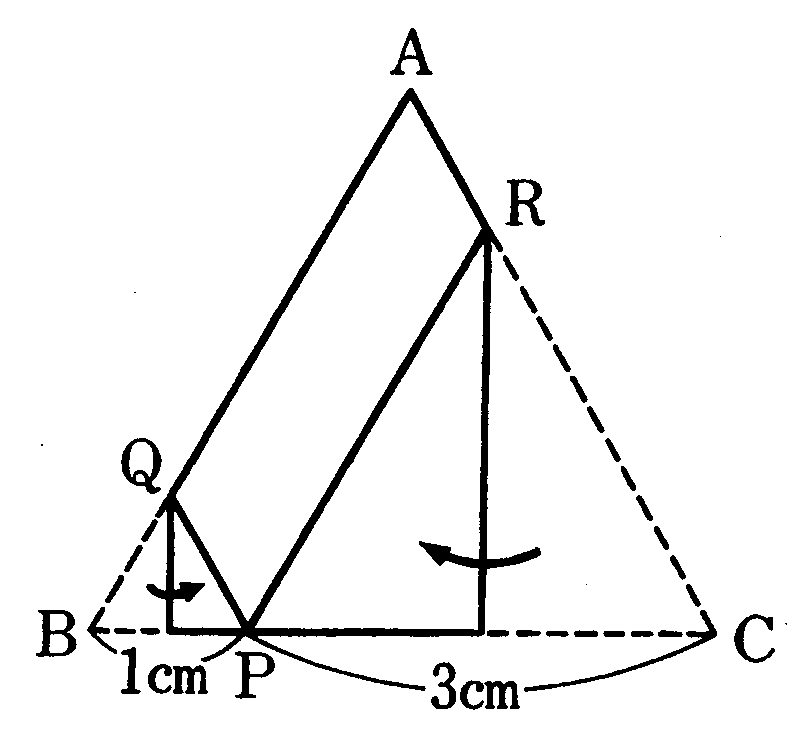
正三角形ABCの面積を1とすると、正三角形QBPと正三角形ABCは相似だから、その面積は1/4 × 1/4=1/16にあたり、同様に正三角形RPCの面積は3/4 × 3/4=9/16にあたる。よって、この五角形の面積は正三角形ABCの面積の1-(1/16 + 9/16)÷2=11/16(倍)になる。
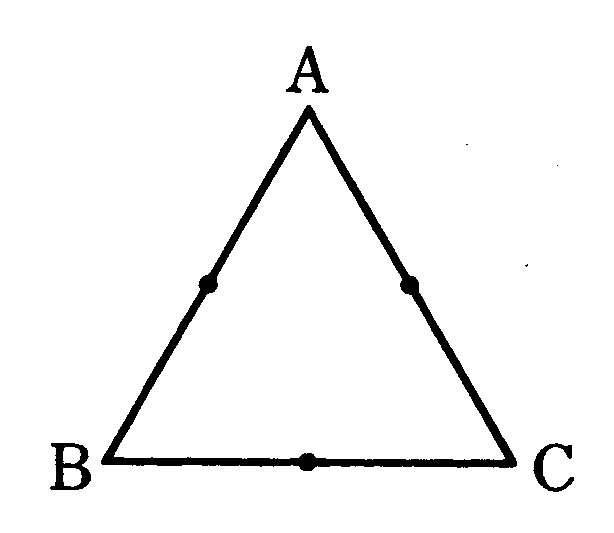
(2) Pが正三角形ABCの中央付近にあるときは、六角形ができる。
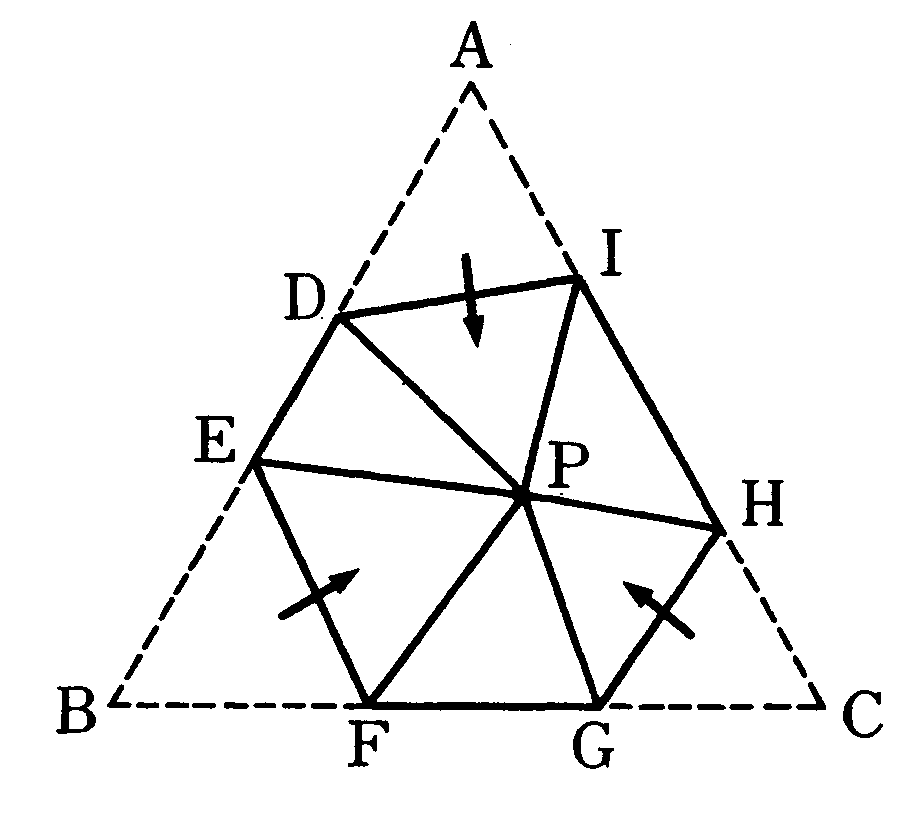
折ってできた図形が長方形になるためには辺DE、FG、HIのうち、辺が2本なくなればよい。かりに辺DE、HIをなくすとき、AD=PD=PE=BEより、D(E)はABの中点になり、同様にH(I)はACの中点になるから、下の図のように点PがBCの中点になれば、折ってできた図形は長方形になる。
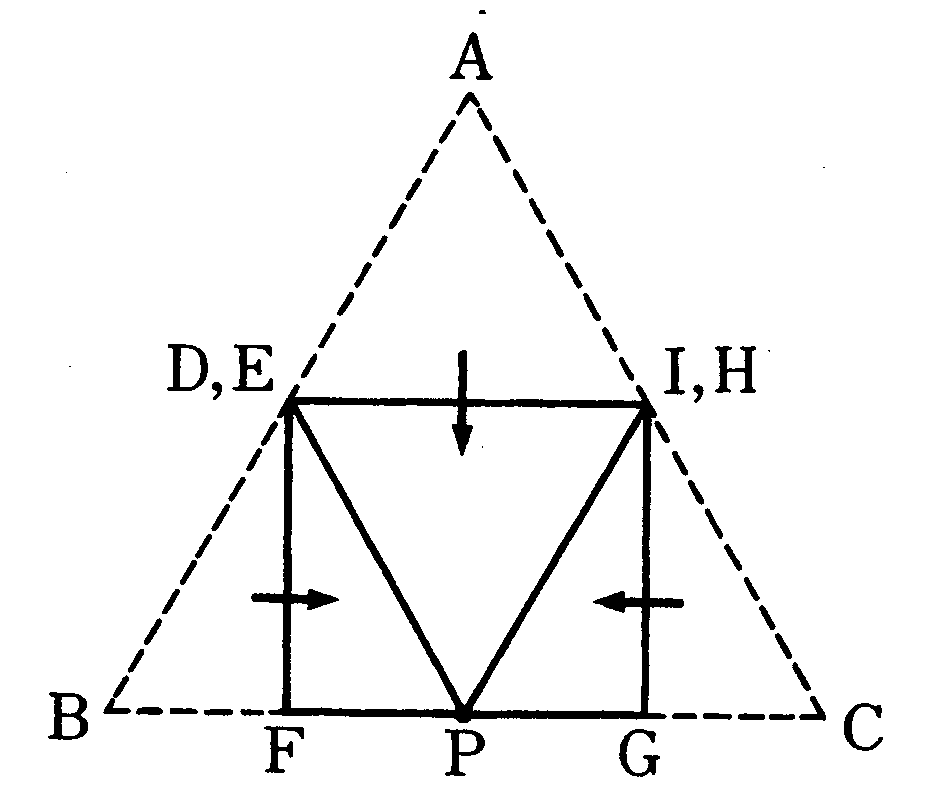
したがって、Pの位置として考えられる場所は辺AB、BC、CAの中点となる。
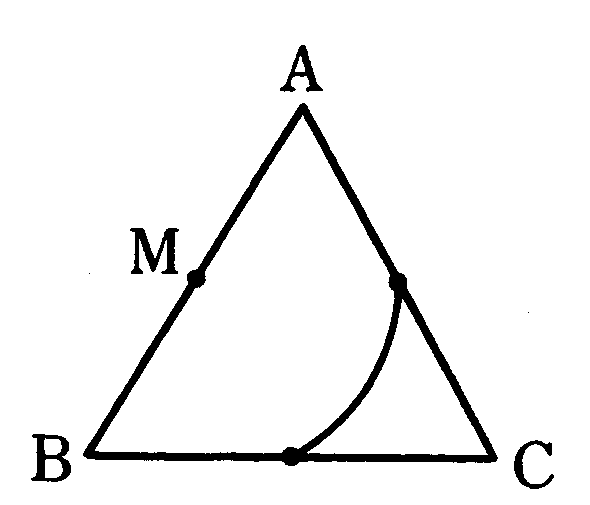
(3)下の図でAM=BM=PMだから、PはMからつねに一定の距離にある。
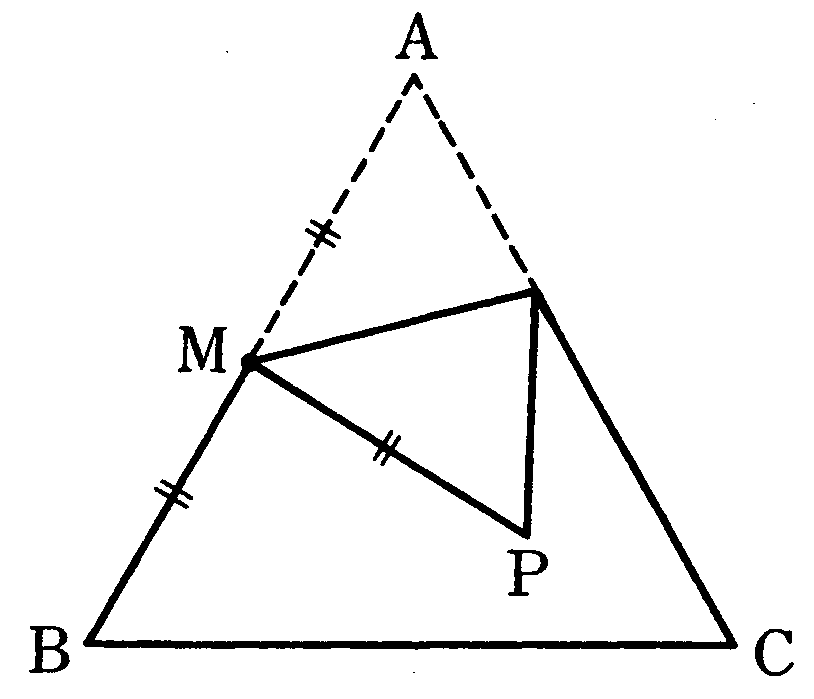
したがって、Pの位置として考えられるのはABを直径とする円周のうち、正三角形ABCからはみ出ない部分と頂点Bである。
(1)
(2)

(3)

【解説】
(1) 折ってできた図形は下の図のような五角形になる。

正三角形ABCの面積を1とすると、正三角形QBPと正三角形ABCは相似だから、その面積は1/4 × 1/4=1/16にあたり、同様に正三角形RPCの面積は3/4 × 3/4=9/16にあたる。よって、この五角形の面積は正三角形ABCの面積の1-(1/16 + 9/16)÷2=11/16(倍)になる。
(2) Pが正三角形ABCの中央付近にあるときは、六角形ができる。

折ってできた図形が長方形になるためには辺DE、FG、HIのうち、辺が2本なくなればよい。かりに辺DE、HIをなくすとき、AD=PD=PE=BEより、D(E)はABの中点になり、同様にH(I)はACの中点になるから、下の図のように点PがBCの中点になれば、折ってできた図形は長方形になる。

したがって、Pの位置として考えられる場所は辺AB、BC、CAの中点となる。
(3)下の図でAM=BM=PMだから、PはMからつねに一定の距離にある。

したがって、Pの位置として考えられるのはABを直径とする円周のうち、正三角形ABCからはみ出ない部分と頂点Bである。
いかがでしたでしょうか。
今回は該当学年でも解ける筑駒の入試問題をご紹介しました。
紙に書くだけでなく、実際に紙を折ったり切ったりして、解くこともできたのではないでしょうか。
この問題に限らず、やってみた!できた!という感覚を大切に取り組んでほしいと思います。
また機会がありましたら、ブログで問題をご紹介します。
それではまたお会いしましょう。
