あけましておめでとうございます。本年もどうぞよろしくお願いいたします。
今週より年明け最初の授業が始まっています。新年を迎え気持ちを新たにがんばりましょう！

さて、今年もエルカミノより生徒一人ひとりへ年賀状を送らせていただきました。
エルカミノの年賀状は、先生方直筆のコメントと一緒に、オリジナルの算数問題を載せています。
冬休み中にがんばって問題を解き、授業初日にさっそく説明してくれる子もいました♪

本日は年賀状問題の解答を発表したいと思います。
まずは問題のおさらいです。

 0 ⃣のカードと 2 ⃣のカードがそれぞれ４枚ずつあります。
このカードを全てならべて８けたの整数を作ります。
できた整数のうち2020で割り切れる整数をすべて答えなさい。
ただし、0で始まる整数(例:02220200など)を作ってはいけません。

正解はこちら
　↓
　↓
　↓
　↓
　↓
　↓
　↓
　↓
　↓
　↓
　↓

 

【解答】20020220，20202020，20220200，22020020，22220000

【解説】

2020＝20×101なので、20の倍数のうち101の倍数でもある数を探します。
20の倍数を探すのは簡単ですが、101の倍数を探すのはちょっと大変です。
そこで、今回は101で割ったときの余りを利用する方法で解いてみます。

4個の 0 ⃣ と4個の 2 ⃣の並びかえで8桁の数字を作ることは、
「2」「20」「200」「2000」「20000」「200000」「2000000」「20000000」
から4個を選んでその和を求めることに置きかえて考えることができます。
例えば 2 ⃣ 0 ⃣ 0 ⃣ 2 ⃣ 2 ⃣ 0 ⃣ 2 ⃣ 0 ⃣であれば20000000＋20000＋2000＋20と置きかえられます。
もちろん「2」は（20の倍数をつくりたいので）選べませんし、「20000000」は必ず選ぶことになるので，実際には「20」～「2000000」から3個を選ぶことを考えることになります。

さて、これらの数を101で割ったときの余りを考えると、

「2」… 2

「20」… 20

「200」… 99

「2000」… 81

などとなりますが、より大きい「20000」のような数を直接101で割るのは大変ですね。
しかし、その余りだけを考えるならそれほど難しいことではありません。
例えば「2000」を10倍した「20000」について、101で割った余りがいくつになるかを考えてみましょう。「2000÷101」の余りが81ですから、81を10倍した答えをもう一度101で割れば「20000」の余りが求められるはずです。

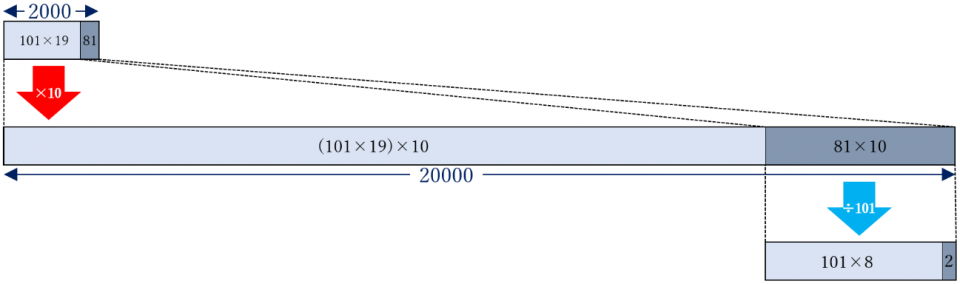
2000÷101＝19余り81
81×10÷101＝8余り2
以上から「20000」の余りは2です。

同様に考えると、101で割ったときの余りは

　「200000」… 20

　「2000000」… 99

　「20000000」… 81

となります。

あとは余りの合計が101の倍数になるような組み合わせを考えればよいので、
20020220，20202020，20220200，22020020，22220000
の5個が答えとなります。
みなさん正解しましたでしょうか？

1月13日(月・祝)には塾生と一般生を対象としたエルカミノ模試を開催いたします。
御三家・筑駒の入試傾向分析から作成した、エルカミノ独自の模擬試験です。
まだ申し込まれていない方はこちらからお申し込みくださいませ。

それではまたお会いしましょう！